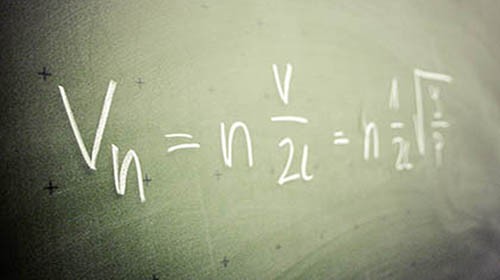3. L’élégance de l’équation
Dominique Moulon débutera ce chapitre en interrogeant le mathématicien sur « l’élégance de l’équation » : que signifie cette expression ? Qu’est-ce qui rend une équation élégante ? Est-ce sa part synthétique ? Est-ce sa forme ? À quel moment et pourquoi parler d’élégance pour qualifier une équation ? Pour répondre à ces questions, Cédric Villani citera Aristote puis partira de l’exemple de l’équation de la gravitation universelle de Newton. En outre, est-il possible d’envisager des grands mathématiciens sans créativité ? Le mathématicien répondra par la négative en citant Poincaré : « La faculté qui permet de développer, c’est l’intuition. Sans elle, le géomètre serait comme un romancier qui serait ferré sur la grammaire et qui n’aurait aucune imagination ». Quels sont les points de convergence entre mathématique et musique ? Pourquoi les associer ? Est-ce pour une question d’harmonie, d’approche ? Est-ce lié à la gestion du rythme ? Enfin, quels sont les rapports établis entre mathématique et peinture ? Plus précisément, pourquoi le nombre d’or « la divina proportione » est-il si présent dans le champ des arts plastiques ?